Random and fixed effect models
In meta-analysis, it is common to talk about random- and fixed-effect models. This can get pretty confusing, because fixed- and random-effects models exist outside meta-analysis as well. As a result, there is a short and a long answer to this (and they don’t entirely agree).
The short answer
In meta-analyses, fixed effect models usually assume that the treatment effect is fixed across studies. Random effects models allow the treatment effect to vary across studies. This, to some extent, accounts for slight random variations in the patient groups across studies that may affect treatment response.
Random effects analyses are not suitable for ‘controlling for’ systematic differences between patient populations. Formal approaches such as meta-regression should be used if measured differences are present.
The long answer
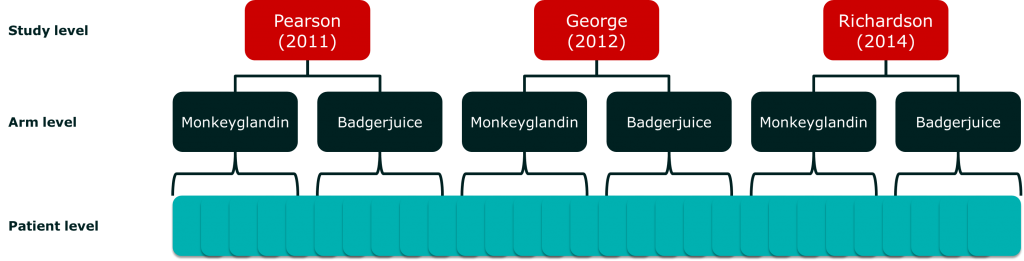
The terms ‘fixed’ and ‘random’ refer to the values of variables within a study or analysis. To illustrate this, let’s use a meta-analysis as an example. Imagine we have a few studies comparing a very exciting new drug, Monkeyglandin, with the current standard therapy, Badgerjuice. If we’re looking at clinical response, we have a number of patients within treatment arms which are, in turn, within studies. In statistical terms, the patients are nested within arms, which are nested within studies:
Our meta-analytic model attempts to incorporate the effect of each level, and the potential interactions between them. Unfortunately, we don’t usually have access to individual patient data, so we have to model aggregate data. These are sample statistics, like means, that describe the sample, but do not contain all the information about it.
If we concentrate on the study and arm variables, we can look at the variable options we have:
- Study level
- Pearson (2011)
- George (2012)
- Richardson (2014)
- Arm level
- Monkeyglandin
- Badgerjuice
At the arm level, we have chosen our treatments to answer a specific study question. In contrast, at the study level, we have selected a sample of studies. The sample may include all the studies currently available, but we could easily imagine another study being produced that is not in our review. In contrast, an additional treatment option could not be added without changing our review question.
Essentially, our options at the arm level are fixed while our options at the study level are sampled from a larger population. In a random effects analysis, we assume that random variables are sampled at random from a larger population. This is one of the many reasons why we have to be careful about how we identify studies to include in a meta-analysis.
So, a fixed effect variable is selected, while a random effect variable is sampled from a population. How does this relate to our meta-analytic model?
Fixed and random effects in a meta-analytic model
The meta-analytic model I started with in this post, looked like this:
(1) ![]()
This is a fixed effect model because the treatment effect is fixed and we are not assuming it is sampled from a wider population of treatment effects. In meta-analyses of efficacy, we usually only refer to the treatment effect when we distinguish between fixed and random effect models. This can cause confusion, as we will see later.
To turn this into a random effect model, we would make one slight change. See if you can spot it. Here’s the random effect model:
(2) ![]()
If you look carefully, you will see that ![]() has changed to
has changed to ![]() . What this means is that the treatment effect
. What this means is that the treatment effect ![]() , rather than only being allowed to vary between treatments, is now allowed to vary within the same treatment between studies.
, rather than only being allowed to vary between treatments, is now allowed to vary within the same treatment between studies.
For it to be a true random effect analysis, we actually have to go a little further and describe the population from which we are sampling:
(3) ![]()
You are probably now thinking: “What? I thought we just said that treatment effects are fixed because we choose them instead of sampling them from a population. This is insanity, I tell you!”
This is the problem with digging into things. They can get a little complicated.
Fortunately, the rationale is actually quite simple, if a little subtle. Each patient will vary in their response to a treatment. If different studies differ slightly in the recruitment of patients, the response of the patients in their sample will vary slightly. This means that, instead of their being just two options at the treatment level, we are actually sampling from a much larger set of possible treatment effects.
The consequence of all this is that, for a fixed effects analysis to be legitimate, we really have to assume that all the patients in all the studies could equally well have been patients in one of the other studies. Often, this is a tricky assumption to make. In these situations, we may choose to use a random effect analysis.
The random effects analysis assumes that there is a true population of treatment effects, which has a mean I am referring to as ![]() and that the treatment effects we observe are randomly sampled from this population of effects.
and that the treatment effects we observe are randomly sampled from this population of effects.
Should I use a random- or a fixed-effects model?
Who knows? The habit appears to have developed of people referring to random-effects models as more conservative because the confidence intervals (or credible intervals in Bayesian stats) are usually larger to account for the additional between-studies uncertainty.
This is true and untrue at the same time. It does reduce the chance of getting a statistically significant result, and so may be more conservative if you are a drug company trying to show that your treatment is more effective than another. However, the lack of a statistically significant difference is not evidence that there is no difference. It just leaves us in a sort of inferential limbo where we don’t know what is going on. This makes the lives of clinicians (who are often taught to worship the significance test) more difficult.
The correct approach to random- and fixed-effects is to choose the statistical model that is most plausible (before you do the test!). Then, you may take a look at alternative models to see how sensitive your analysis is to the assumptions you have had to make. Note that I say ‘models’. The random-effects model is just one of many models that are possible. Actually, there are an infinite number of possible models. Really, when you believe that there is heterogeneity in the treatment effect across studies, you should try to work out what’s causing it and handle that instead.
Why should I try and find heterogeneity rather than just use a random-effects model?
Look at your assumptions. Can you really, honestly, say that the random effect is distributed randomly around some population mean? How can you say that?
If there is a single cause of the observed heterogeneity, it is unlikely to be randomly distributed in the available studies. Even if it is, the number of studies is usually quite small, so you get the problem of lumpy probability and poor estimation of the underlying parameter (![]() ).
).
Choosing a statistical model is not a trivial process. The great advantage we have nowadays is that it is getting easier to build our own statistical models, rather than relying on pre-packaged statistical tests. This allows us to be a bit more picky.
Are there other random effect models in meta-analysis?
Usually, because we are looking at comparative data, we assume that the study level effect is effectively a nuisance variable. We can work it out by fixing one treatment effect (usually placebo) to 0 and doing the sums. For most of my career, I have been happy to take this approach and only look at study level effects to check for evidence of inconsistency between studies.
However, a colleague recently showed me that this can produce some pretty weird results. Specifically, there are some disease areas where you get asymmetrical distributions for treatment effects using normal meta-analytic models. What he suggested was putting a random effect on the study level effect. The model looks something like this (when simplified):
(4) ![]()
(5) ![]()
What this model does is to constrain the study level effect. It does require that we assume that the studies are sampled at random from the population of potential studies, but that is really a required assumption for meta-analyses anyway (as explained above). I am a little wary of it because it feels like it is constraining the study-level effects to manage problems with the available data. However, in some situations it avoids results that are nonsensical, and allowing study-level effects to vary wildly to get data to fit a statistical model is also dodgy.
This type of model is known as a random intercept model, because the random effect is on the intercept of the regression equation. If you want to learn more about it, there’s some interesting stuff on the Bristol university site.
It’s an interesting approach, but what it highlights is the inconsistency in terminology. A lot of meta-analysts would refer to the equation above as a fixed effects model because the treatment effect is fixed. However, it is a random effect model in the wider world of statistical analysis.
Summary
Random effects are effects that we believe to be sampled from a population of possible effects. Fixed effects include the entire population of interest. In practical terms, this means that fixed effects are usually the effects we fix as part of our study design.
Meta-analyses with random treatment effects are sometimes treated like a panacea for uncertainties about the comparability of studies. They are not and, in general, my preference is for fixed treatment effects. However, not everyone would agree. Most statistical models will include components that are fixed alongside random components. As with all statistical modelling, careful consideration of competing modelling approaches is more important than some standard catch-all ruling.

Leave a Reply
You must be logged in to post a comment.