Bayesian approaches to statistics use simple ideas about contingent probability (i.e. the probability of one thing, given that another thing is true). They extend these ideas to look at the extent to which we should believe one thing, given a set of observed data. The important consequence of this is that they tell us how we should update our beliefs as data becomes available.

They are, I would argue, a natural extension of standard frequentist statistical approaches and are not scary or weird.

The people who use them, I’m less sure about.

That’s the short answer. Here’s the long answer:

The long answer

Understanding the Bayesian approach is actually not that complex. It just requires a little bit of thinking. First, we’ll start with a bit of probability.

Probability

There are lots of ways of thinking about probability, and some of them involve horribly complex-looking mathematical expressions involving set theory. My central claim is that Bayesian statistics is a consequence of frequentist statistics, so let’s start with a classic frequentist statistical description.

Frequentist approaches to probability are based around the idea that, over long runs of events or in large samples, things tend to happen in a broadly predictable manner. What does that mean? Well, if I had a coin and I flipped it a couple of times, you wouldn’t be surprised if I got two heads (100% heads). However, if I flipped it 1,000 times, you would be surprised if I got 1,000 heads (still 100% heads). You would expect me to get heads about 500 times. You wouldn’t expect it to be exactly 500, but something like that.

The frequentist approach is to say that, the more I flip the coin, the closer the proportion of flips will be to 0.5. Let’s express that mathematically:

$\begin{equation*}\ \lim_{n \to \infty} {{a}\over {n}} = p \end{equation}$

where a is the number of heads, n is the number of coin tosses, and so p is the proportion of heads.

The expression just states that, as the number of coin flips approaches infinity, the proportion that are heads approaches p. Our expectation is that p is 0.5.

Coin tosses are (usually) fairly trivial. We tend to be more interested in situations where the probabilities are less obvious. Let’s use something a bit more relevant to our own problems. Let’s use breast cancer.

What is the probability of getting breast cancer?

According to the ONS, there were 41,826 malignant neoplasm of the breast (i.e. breast cancer) cases registered in 2011. At the time, the population of the UK was 63.2 million, including 31 million men and 32.2 million women.

That means that the risk of getting a breast cancer diagnosis in 2011 in the UK was about 0.00066, or 66 in every 100,000 people. We can look at this using a simple Venn Diagram showing all the people with a new breast cancer diagnosis and all the people who live in the UK.

Rendered by QuickLaTeX.com

$\begin{equation*}\ {P(cancer)}={{{Area_{red}} \over{Area_{red}+{Area_{blue}}}}={{{(UK\,population)} \cap {(Breast\,cancer)}} \over {UK\,population}} \end{equation}$

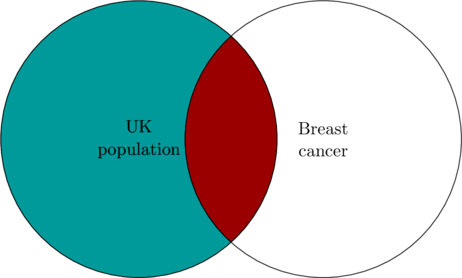
The thing is, we aren’t really interested in the risks in the general population. We want to know what our risk is. This is much more difficult.

In the fullness of time, we will know our individual risk, because we will either get a breast cancer diagnosis or not. Until that fateful day, we can only guess. Statistics is the tool we use to make that guess.

In this case, we may decide that we have characteristics that should allow us to estimate the probability of a breast cancer diagnosis more precisely. A pretty obvious example of this is sex.

Of the 41,826 registered cases of breast cancer, 41,523 were amongst women. That means that the incidence rate in women was approximately 0.0013, or 130 in every 100,000 women.

Contingent probability

Contingent probability is simply the probability of one thing given something else.

Contingency in probability implies that two events or pieces of information are not independent. In our breast cancer example, the risk of breast cancer is clearly influenced by sex.

If we take the Venn diagram we produced earlier and split the UK population in two, you can see that the general approach to calculating this new probability is similar to what we did before in that an estimate of the probability that you receive a breast cancer diagnosis given that you are a woman ( $P(cancer|female)$ ) can be calculated by taking the number of people who are woman and have a breast cancer diagnosis ( $P(female \cap cancer)$ ) and dividing it by the total number of women ( $P(female)$ ):

Rendered by QuickLaTeX.com

$\begin{equation*}\ {P(cancer|female)}={{{(UK\,female\,population)} \cap {(Breast\,cancer)}} \over {UK\,female\,population}} \end{equation}$

If you look at the way we calculated the risk originally, this is precisely the same. That’s an important point. All statistics involves contingency. It’s just that it only becomes apparent occasionally.

Bayes’ rule

Some of the most astounding scientific insights in history can be worked out using simple substitutions and rearrangements of the type we do in high school.

This is one of those nice, easy, examples.

The late 17th and early 18th century was a pretty exciting time for science. Newton and Leibniz developed calculus (although Newton called it fluxions and fluents), the Royal Society was founded, and a whole host of fundamental scientific discoveries were made. As the 17th century drew to a close and the 18th century gathered pace, the ideas developed by people like Newton started to be published and discussed more widely. One of those involved in this discourse was a Presbyterian minister called Thomas Bayes.

Bayes was a member of the Royal Society and had written on Newton’s work. In his spare time, he also managed to invent a new approach to statistics, although it’s not clear whether this was deliberate.

Bayes took the simple probability statements we talk about above, and turned them into a rather neat little theorem. We can work this one out ourselves:

We start with a generalised version of what we discussed with Venn diagrams and its converse:

(1) $\begin{equation*} {P(A|B)}={{{P(A} \cap {B)}} \over {P(B)}} \end{equation*}$

(2) $\begin{equation*} {P(B|A)}={{{P(B} \cap {A)}} \over {P(A)}} \end{equation*}$

We can rearrange equation 2 to get an expression for the intersect of A and B:

$\begin{equation*} {P(B|A)}={{{P(B} \cap {A)}} \over {P(A)}} \end{equation}$

(3) $\begin{equation*} \therefore {{P(B|A)} \times {P(A)}}} = {{{P(B} \cap {A)}} \end{equation*}$

Then we can substitute it for the intersect value in equation 1:

$\begin{equation*} {P(A|B)}={{{P(A} \cap {B)}} \over {P(B)}} \end{equation}$

(4) $\begin{equation*} \therefore {P(A|B)} = {{{P(B|A)} \times {P(A)}} \over {P(B)}}} \end{equation*}$

This expression is known as Bayes’ theorem.

While this is simple to derive, it is not immediately apparent what it means or what its value is. To show that, we’ll run through the breast cancer analysis again.

If we substitute cancer for A and female for B, we get:

$\begin{equation*} {P(cancer|female)} = {{{P(female|cancer)} \times {P(cancer)}} \over {P(female)}}} \end{equation}$

We have the numbers to populate this already:

$\begin{equation*} {P(cancer|female)} &= {{{{41523} \over {41826}} \times {{41826} \over {63200000}}} \over {{32200000} \over {63200000}}} &= {{{{41523} \over {\cancel{41826}}} \times {{{\cancel{41826}} \over {{\cancel{63200000}}}} \over {{32200000} \over {\cancel{63200000}}}} &= {{41523} \over {32200000}} &= {0.0013} \end{equation}$

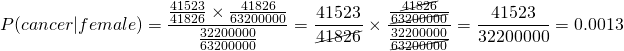
In other words, we get precisely the same result as we did before. It just looks like a slightly more complex way of going about it.

The probability of truth

Why on Earth would anyone choose to use a more complex equation to answer a simple question? After all, we managed to calculate a breast cancer risk using much a more simple approach.

This is a fair question. The basic answer is that we have a lot of information about breast cancer, so it is comparatively easy to perform the calculations (although an epidemiologist would hate they way we’ve done it!).

The more subtle answer is to look at what we’re really doing. Our initial estimate of risk was based on imperfect information; we just knew our subject was in the UK. We then updated that assessment based on more information. What Bayes’ theorem tells us is how to update our estimates based on fresh information. We can take this even further and use it to look at how we should change our beliefs as information becomes available.

To do this, we replace A and B with H and E, where H is a hypothesis and E is some evidence:

(5) $\begin{equation*} {P(H|E)} = {{{P(E|H)} \times {P(H)}} \over {P(E)}}} \end{equation*}$

What this tells us is that we can assess the probability of a hypothesis being true (i.e. how much we should believe a hypothesis – $P(H|E)$ ) if we know:

The probability of observing our evidence if the hypothesis is true, $P(E|H)$
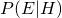
The probability of our hypothesis being true independent of the evidence, $P(H)$
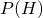
The probability of observing the evidence under all possible hypotheses, $P(E)$

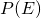
$P(H)$ is referred to as the prior because it describes what we believe prior to the evidence being available. $P(E|H) \over P(E)$ is the extent to which the evidence supports the hypothesis. It can be thought of as a weighting reflecting the extent to which the evidence would be observed under this hypothesis versus any other hypothesis. Finally, $P(H|E)$ is referred to as the posterior because it reflects what we should believe based on our prior belief about the hypothesis and the degree of support provided by the fresh evidence to that hypothesis.

Common examples used to explain Bayesian statistics include diagnostic tests and, most commonly, the Monty Hall Problem. Just to be clear – you don’t need Bayesian statistics to solve the Monty Hall problem or to investigate screening campaigns. You just need contingent probability or a simple decision tree.

Where Bayesian statistics really comes into its own is when we have to make decisions based on imperfect information. This describes most decision problems. In these situations, a Bayesian analysis will be at least as good as a frequentist analysis, and may be better.

Hold on a second, how can I say that it will be at least as good as a frequentist analysis?

The observation that we got the same answer using Bayes’ theorem as we did by direct calculation is important. If we use prior information that is accurate and sensible models for estimating the marginal probability of E, our results will match an equivalent frequentist analysis. The reason for this is that Bayesian statistics is a consequence of frequentist statistics, not a separate method.

If you’re a statistics expert and you know better, please feel free to flame me horrendously for this claim by commenting below.

For those of you wanting an example of applied Bayesian statistics, screening is a comparatively simple application.

Strengths and weaknesses of Bayesian statistics

Now, I consider myself a proponent of Bayesian methods. I love the fact that Bayesian analyses give you a directly interpretable distributions describing the uncertainty of your beliefs. Uncertainty is fundamental to an honest appraisal of the world, and quantifying it so that you can manage it is a hugely powerful gift. However, Bayesian methods are not always the best way to handle data.

Bayesian approaches often require quite a lot of computing effort. The detail on this is for another post, but we often resort to simulation-based approaches to solve the equations Bayesian statistics leaves us with. If you’re just trying to calculate a crude number based on available data, this can be a waste of time. I could counter this by saying that not all Bayesian analyses are complex. Some are both insightful and simple. I could also point out that plenty of other statistical approaches are complex, but that misses the point a bit.

Another common complaint is that Bayesian methods are driven by prior beliefs. This is slightly disingenuous in that the prior belief can be expressed strongly or weakly, and can be based on whatever evidence you have available. Bayesian approaches are susceptible to being driven by biased priors, particularly where the data are unclear. The thing is, it is easy to test this; just redo the analysis with a different prior.

The strengths I see in Bayesian approaches are really about the ability to update beliefs very rapidly as data comes in, and the ability to incorporate different types of information in an analysis. This allows us to deal with complex analytic situations in a way that makes use of available expertise.

My overall recommendation is that you use the simplest statistical approach you can justify to achieve the ends you need. Generally, I think the reason people disagree on approaches is that it’s hard work learning statistics, and so the simplest statistical approach is often the one you use most commonly, whether that’s Bayesian or frequentist. The same problem occurs with choosing a statistics programme to use.

Bayesian statistics