Ebola screening
What are the arguments over ebola screening really about? Here’s my go at explaining, with a bit of help from the Reverend Bayes.
There’s a lot of fear and uncertainty about the potential spread of ebola at the moment, and some countries have started screening new arrivals at airports and other ports of entry for signs of ebola.
There are several ways of running a screening programme of this type, and arguments persist about whether screening is appropriate or works. Some of the arguments are actually quite subtle and difficult to convey in the short time available on a news channel. Here’s my attempt to discuss things in a little more detail.
Bayesian statistics can help us understand screening and, importantly, can help us break down the arguments so that we can understand when it is worthwhile and how it can best be done.
When a person is screened for ebola, one of four situations can arise:
| H | |||
|---|---|---|---|
| E | Has ebola (H) | Does not have ebola (not H) | |
| Positive screen result (E) | True positive | False positive | |
| Negative screen result (not E) | False negative | True negative | |
What Bayes’ theorem can do is help us to understand the relationship between screen results and ebola status. There’s a detailed explanation of Bayes’ theorem in the glossary, but for now we just need the equation:
(1) ![]()
Where:
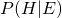 is the probability that you have ebola given a positive screen
is the probability that you have ebola given a positive screen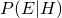 is the probability that you get a positive screen given that you have ebola. This is known as the sensitivity of the test
is the probability that you get a positive screen given that you have ebola. This is known as the sensitivity of the test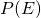 is the probability of getting a positive screen regardless of whether you have ebola or not
is the probability of getting a positive screen regardless of whether you have ebola or not
![]() is a bit of a complex concept, but it can be broken down to make it more manageable:
is a bit of a complex concept, but it can be broken down to make it more manageable:
(2) ![]()
This is simply the probability of getting a positive screen if you have ebola plus the probability of getting a positive screen if you don’t have ebola, each of which scaled by the chance that you have, or do not have, ebola.
In equation 2, ![]() is the chance of getting a positive screen if you do not have ebola. This is related to the specificity of a test.
is the chance of getting a positive screen if you do not have ebola. This is related to the specificity of a test.
Given some basic information about the ebola test, we can start to populate our table. Specifically, we need to the sensitivity of the test and its specificity.
Now, I don’t know the sensitivity and specificity of current ebola tests, but the CDC appears to suggest that real-time PCR methods are used. This paper, which is quite old so may not reflect current practice, suggests a sensitivity of between 91% and 100% and a specificity of around 97% for real-time PCR. Therefore, without further information, my guess would be that a full laboratory test is about 95% sensitive and 97% specific to ebola.
We can use this to populate some equations:
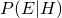 is the sensitivity, which we believe is about
is the sensitivity, which we believe is about 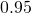
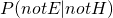 is the specificity, which is about
is the specificity, which is about 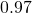
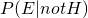 is one minus the specificity, which is
is one minus the specificity, which is 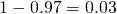
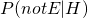 is one minus the sensitivity, which is
is one minus the sensitivity, which is 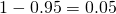
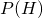 is the prior probability of having ebola. In this case, that means the probability of having ebola before we know the test results. Obviously, this is going to vary between people, so I’ll leave it blank for now
is the prior probability of having ebola. In this case, that means the probability of having ebola before we know the test results. Obviously, this is going to vary between people, so I’ll leave it blank for now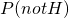 is
is 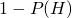 , because a person must either have, or not have, ebola
, because a person must either have, or not have, ebola
The important thing now is that we have enough data to calculate the cells in our table. Furthermore, we can do this for a whole range of values of ![]() . That means, we can look at the value of ebola tests for people with a whole range of baseline risks. We can also look at the data two ways:
. That means, we can look at the value of ebola tests for people with a whole range of baseline risks. We can also look at the data two ways:
- From the patient perspective – For example,
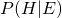 is the probability that you have ebola given a positive test. We can look at all the data this way to explain to people going through the test process why they should, or should not, rely heavily on the test
is the probability that you have ebola given a positive test. We can look at all the data this way to explain to people going through the test process why they should, or should not, rely heavily on the test - From a public health perspectve – For example, if we look at
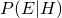 , we can see how useful our test is at catching cases from high risk areas
, we can see how useful our test is at catching cases from high risk areas
We will start with the patient perspective.
The graphs below show how confident we should be in a positive (graph 1) and negative (graph 2) diagnostic test. The x-axis is ![]() , which is their baseline risk. In other words, this is the risk they had of ebola prior to us performing the test.
, which is their baseline risk. In other words, this is the risk they had of ebola prior to us performing the test.
Graph 1
[chartboot version= ‘3.0’ code= ‘4A86’ border= ‘1’ width= ‘800’ height= ‘400’ attribution= ‘1’ jsondesc= ‘{“containerId”:”visualization4A86″,”dataTable”:{“cols”:xxx00xxx{“id”:””,”label”:”Prior probability of ebola”,”pattern”:””,”type”:”string”,”p”:{}},{“id”:””,”label”:”True positive”,”pattern”:””,”type”:”number”,”p”:{}},{“id”:””,”label”:”False positive”,”pattern”:””,”type”:”number”}xxx01xxx,”rows”:xxx00xxx{“c”:xxx00xxx{“v”:”0″,”f”:null},{“v”:0,”f”:null},{“v”:1000,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.01″,”f”:null},{“v”:242,”f”:null},{“v”:758,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.02″,”f”:null},{“v”:393,”f”:null},{“v”:607,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.03″,”f”:null},{“v”:495,”f”:null},{“v”:505,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.04″,”f”:null},{“v”:569,”f”:null},{“v”:431,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.05″,”f”:null},{“v”:625,”f”:null},{“v”:375,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.06″,”f”:null},{“v”:669,”f”:null},{“v”:331,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.07″,”f”:null},{“v”:704,”f”:null},{“v”:296,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.08″,”f”:null},{“v”:734,”f”:null},{“v”:266,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.09″,”f”:null},{“v”:758,”f”:null},{“v”:242,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.1″,”f”:null},{“v”:779,”f”:null},{“v”:221,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.11″,”f”:null},{“v”:796,”f”:null},{“v”:204,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.12″,”f”:null},{“v”:812,”f”:null},{“v”:188,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.13″,”f”:null},{“v”:826,”f”:null},{“v”:174,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.14″,”f”:null},{“v”:838,”f”:null},{“v”:162,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.15″,”f”:null},{“v”:848,”f”:null},{“v”:152,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.16″,”f”:null},{“v”:858,”f”:null},{“v”:142,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.17″,”f”:null},{“v”:866,”f”:null},{“v”:134,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.18″,”f”:null},{“v”:874,”f”:null},{“v”:126,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.19″,”f”:null},{“v”:881,”f”:null},{“v”:119,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.2″,”f”:null},{“v”:888,”f”:null},{“v”:112,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.21″,”f”:null},{“v”:894,”f”:null},{“v”:106,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.22″,”f”:null},{“v”:899,”f”:null},{“v”:101,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.23″,”f”:null},{“v”:904,”f”:null},{“v”:96,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.24″,”f”:null},{“v”:909,”f”:null},{“v”:91,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.25″,”f”:null},{“v”:913,”f”:null},{“v”:87,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.26″,”f”:null},{“v”:918,”f”:null},{“v”:82,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.27″,”f”:null},{“v”:921,”f”:null},{“v”:79,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.28″,”f”:null},{“v”:925,”f”:null},{“v”:75,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.29″,”f”:null},{“v”:928,”f”:null},{“v”:72,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.3″,”f”:null},{“v”:931,”f”:null},{“v”:69,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.31″,”f”:null},{“v”:934,”f”:null},{“v”:66,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.32″,”f”:null},{“v”:937,”f”:null},{“v”:63,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.33″,”f”:null},{“v”:940,”f”:null},{“v”:60,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.34″,”f”:null},{“v”:942,”f”:null},{“v”:58,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.35″,”f”:null},{“v”:945,”f”:null},{“v”:55,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.36″,”f”:null},{“v”:947,”f”:null},{“v”:53,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.37″,”f”:null},{“v”:949,”f”:null},{“v”:51,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.38″,”f”:null},{“v”:951,”f”:null},{“v”:49,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.39″,”f”:null},{“v”:953,”f”:null},{“v”:47,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.4″,”f”:null},{“v”:955,”f”:null},{“v”:45,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.41″,”f”:null},{“v”:957,”f”:null},{“v”:43,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.42″,”f”:null},{“v”:958,”f”:null},{“v”:42,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.43″,”f”:null},{“v”:960,”f”:null},{“v”:40,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.44″,”f”:null},{“v”:961,”f”:null},{“v”:39,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.45″,”f”:null},{“v”:963,”f”:null},{“v”:37,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.46″,”f”:null},{“v”:964,”f”:null},{“v”:36,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.47″,”f”:null},{“v”:966,”f”:null},{“v”:34,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.48″,”f”:null},{“v”:967,”f”:null},{“v”:33,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.49″,”f”:null},{“v”:968,”f”:null},{“v”:32,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.5″,”f”:null},{“v”:969,”f”:null},{“v”:31,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.51″,”f”:null},{“v”:971,”f”:null},{“v”:29,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.52″,”f”:null},{“v”:972,”f”:null},{“v”:28,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.53″,”f”:null},{“v”:973,”f”:null},{“v”:27,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.54″,”f”:null},{“v”:974,”f”:null},{“v”:26,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.55″,”f”:null},{“v”:975,”f”:null},{“v”:25,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.56″,”f”:null},{“v”:976,”f”:null},{“v”:24,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.57″,”f”:null},{“v”:977,”f”:null},{“v”:23,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.58″,”f”:null},{“v”:978,”f”:null},{“v”:22,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.59″,”f”:null},{“v”:979,”f”:null},{“v”:21,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.6″,”f”:null},{“v”:979,”f”:null},{“v”:21,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.61″,”f”:null},{“v”:980,”f”:null},{“v”:20,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.62″,”f”:null},{“v”:981,”f”:null},{“v”:19,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.63″,”f”:null},{“v”:982,”f”:null},{“v”:18,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.64″,”f”:null},{“v”:983,”f”:null},{“v”:17,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.65″,”f”:null},{“v”:983,”f”:null},{“v”:17,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.66″,”f”:null},{“v”:984,”f”:null},{“v”:16,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.67″,”f”:null},{“v”:985,”f”:null},{“v”:15,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.68″,”f”:null},{“v”:985,”f”:null},{“v”:15,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.69″,”f”:null},{“v”:986,”f”:null},{“v”:14,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.7″,”f”:null},{“v”:987,”f”:null},{“v”:13,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.71″,”f”:null},{“v”:987,”f”:null},{“v”:13,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.72″,”f”:null},{“v”:988,”f”:null},{“v”:12,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.73″,”f”:null},{“v”:988,”f”:null},{“v”:12,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.74″,”f”:null},{“v”:989,”f”:null},{“v”:11,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.75″,”f”:null},{“v”:990,”f”:null},{“v”:10,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.76″,”f”:null},{“v”:990,”f”:null},{“v”:10,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.77″,”f”:null},{“v”:991,”f”:null},{“v”:9,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.78″,”f”:null},{“v”:991,”f”:null},{“v”:9,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.79″,”f”:null},{“v”:992,”f”:null},{“v”:8,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.8″,”f”:null},{“v”:992,”f”:null},{“v”:8,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.81″,”f”:null},{“v”:993,”f”:null},{“v”:7,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.82″,”f”:null},{“v”:993,”f”:null},{“v”:7,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.83″,”f”:null},{“v”:994,”f”:null},{“v”:6,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.84″,”f”:null},{“v”:994,”f”:null},{“v”:6,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.85″,”f”:null},{“v”:994,”f”:null},{“v”:6,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.86″,”f”:null},{“v”:995,”f”:null},{“v”:5,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.87″,”f”:null},{“v”:995,”f”:null},{“v”:5,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.88″,”f”:null},{“v”:996,”f”:null},{“v”:4,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.89″,”f”:null},{“v”:996,”f”:null},{“v”:4,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.9″,”f”:null},{“v”:997,”f”:null},{“v”:3,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.91″,”f”:null},{“v”:997,”f”:null},{“v”:3,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.92″,”f”:null},{“v”:997,”f”:null},{“v”:3,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.93″,”f”:null},{“v”:998,”f”:null},{“v”:2,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.94″,”f”:null},{“v”:998,”f”:null},{“v”:2,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.95″,”f”:null},{“v”:998,”f”:null},{“v”:2,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.96″,”f”:null},{“v”:999,”f”:null},{“v”:1,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.97″,”f”:null},{“v”:999,”f”:null},{“v”:1,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.98″,”f”:null},{“v”:999,”f”:null},{“v”:1,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.99″,”f”:null},{“v”:1000,”f”:null},{“v”:0,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”1″,”f”:null},{“v”:1000,”f”:null},{“v”:0,”f”:null}xxx01xxx}xxx01xxx,”p”:null},”options”:{“legend”:”top”,”title”:”Interpreting positive test results”,”isStacked”:true,”vAxes”:xxx00xxx{“title”:”Number of people”,”minValue”:null,”maxValue”:null,”viewWindow”:{“max”:null,”min”:null},”logScale”:false,”useFormatFromData”:true},{“viewWindow”:{“max”:null,”min”:null},”minValue”:null,”maxValue”:null,”logScale”:false,”useFormatFromData”:true}xxx01xxx,”animation”:{“duration”:500},”booleanRole”:”certainty”,”hAxis”:{“minValue”:null,”maxValue”:null,”viewWindow”:null,”viewWindowMode”:null,”useFormatFromData”:true,”title”:”Baseline risk (prior – P(H))”},”series”:{“0”:{“color”:”#00cc7a”,”areaOpacity”:”0.3″},”1″:{“color”:”#ff9900″,”areaOpacity”:”0.3″}}},”state”:{},”view”:{},”isDefaultVisualization”:false,”chartType”:”AreaChart”}’ ]
Graph 2
[chartboot version= ‘3.0’ code= ‘B043’ border= ‘1’ width= ‘800’ height= ‘400’ attribution= ‘1’ jsondesc= ‘{“containerId”:”visualizationB043″,”dataTable”:{“cols”:xxx00xxx{“id”:””,”label”:”Prior probability of ebola”,”pattern”:””,”type”:”string”,”p”:{}},{“id”:””,”label”:”True negative”,”pattern”:””,”type”:”number”,”p”:{}},{“id”:””,”label”:”False negative”,”pattern”:””,”type”:”number”}xxx01xxx,”rows”:xxx00xxx{“c”:xxx00xxx{“v”:”0″,”f”:null},{“v”:1000,”f”:null},{“v”:0,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.01″,”f”:null},{“v”:999,”f”:null},{“v”:1,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.02″,”f”:null},{“v”:999,”f”:null},{“v”:1,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.03″,”f”:null},{“v”:998,”f”:null},{“v”:2,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.04″,”f”:null},{“v”:998,”f”:null},{“v”:2,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.05″,”f”:null},{“v”:997,”f”:null},{“v”:3,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.06″,”f”:null},{“v”:997,”f”:null},{“v”:3,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.07″,”f”:null},{“v”:996,”f”:null},{“v”:4,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.08″,”f”:null},{“v”:996,”f”:null},{“v”:4,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.09″,”f”:null},{“v”:995,”f”:null},{“v”:5,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.1″,”f”:null},{“v”:994,”f”:null},{“v”:6,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.11″,”f”:null},{“v”:994,”f”:null},{“v”:6,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.12″,”f”:null},{“v”:993,”f”:null},{“v”:7,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.13″,”f”:null},{“v”:992,”f”:null},{“v”:8,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.14″,”f”:null},{“v”:992,”f”:null},{“v”:8,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.15″,”f”:null},{“v”:991,”f”:null},{“v”:9,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.16″,”f”:null},{“v”:990,”f”:null},{“v”:10,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.17″,”f”:null},{“v”:990,”f”:null},{“v”:10,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.18″,”f”:null},{“v”:989,”f”:null},{“v”:11,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.19″,”f”:null},{“v”:988,”f”:null},{“v”:12,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.2″,”f”:null},{“v”:987,”f”:null},{“v”:13,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.21″,”f”:null},{“v”:986,”f”:null},{“v”:14,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.22″,”f”:null},{“v”:986,”f”:null},{“v”:14,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.23″,”f”:null},{“v”:985,”f”:null},{“v”:15,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.24″,”f”:null},{“v”:984,”f”:null},{“v”:16,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.25″,”f”:null},{“v”:983,”f”:null},{“v”:17,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.26″,”f”:null},{“v”:982,”f”:null},{“v”:18,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.27″,”f”:null},{“v”:981,”f”:null},{“v”:19,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.28″,”f”:null},{“v”:980,”f”:null},{“v”:20,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.29″,”f”:null},{“v”:979,”f”:null},{“v”:21,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.3″,”f”:null},{“v”:978,”f”:null},{“v”:22,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.31″,”f”:null},{“v”:977,”f”:null},{“v”:23,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.32″,”f”:null},{“v”:976,”f”:null},{“v”:24,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.33″,”f”:null},{“v”:975,”f”:null},{“v”:25,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.34″,”f”:null},{“v”:974,”f”:null},{“v”:26,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.35″,”f”:null},{“v”:973,”f”:null},{“v”:27,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.36″,”f”:null},{“v”:972,”f”:null},{“v”:28,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.37″,”f”:null},{“v”:971,”f”:null},{“v”:29,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.38″,”f”:null},{“v”:969,”f”:null},{“v”:31,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.39″,”f”:null},{“v”:968,”f”:null},{“v”:32,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.4″,”f”:null},{“v”:967,”f”:null},{“v”:33,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.41″,”f”:null},{“v”:965,”f”:null},{“v”:35,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.42″,”f”:null},{“v”:964,”f”:null},{“v”:36,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.43″,”f”:null},{“v”:963,”f”:null},{“v”:37,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.44″,”f”:null},{“v”:961,”f”:null},{“v”:39,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.45″,”f”:null},{“v”:960,”f”:null},{“v”:40,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.46″,”f”:null},{“v”:958,”f”:null},{“v”:42,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.47″,”f”:null},{“v”:956,”f”:null},{“v”:44,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.48″,”f”:null},{“v”:955,”f”:null},{“v”:45,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.49″,”f”:null},{“v”:953,”f”:null},{“v”:47,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.5″,”f”:null},{“v”:951,”f”:null},{“v”:49,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.51″,”f”:null},{“v”:949,”f”:null},{“v”:51,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.52″,”f”:null},{“v”:947,”f”:null},{“v”:53,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.53″,”f”:null},{“v”:945,”f”:null},{“v”:55,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.54″,”f”:null},{“v”:943,”f”:null},{“v”:57,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.55″,”f”:null},{“v”:941,”f”:null},{“v”:59,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.56″,”f”:null},{“v”:938,”f”:null},{“v”:62,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.57″,”f”:null},{“v”:936,”f”:null},{“v”:64,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.58″,”f”:null},{“v”:934,”f”:null},{“v”:66,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.59″,”f”:null},{“v”:931,”f”:null},{“v”:69,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.6″,”f”:null},{“v”:928,”f”:null},{“v”:72,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.61″,”f”:null},{“v”:925,”f”:null},{“v”:75,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.62″,”f”:null},{“v”:922,”f”:null},{“v”:78,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.63″,”f”:null},{“v”:919,”f”:null},{“v”:81,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.64″,”f”:null},{“v”:916,”f”:null},{“v”:84,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.65″,”f”:null},{“v”:913,”f”:null},{“v”:87,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.66″,”f”:null},{“v”:909,”f”:null},{“v”:91,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.67″,”f”:null},{“v”:905,”f”:null},{“v”:95,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.68″,”f”:null},{“v”:901,”f”:null},{“v”:99,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.69″,”f”:null},{“v”:897,”f”:null},{“v”:103,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.7″,”f”:null},{“v”:893,”f”:null},{“v”:107,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.71″,”f”:null},{“v”:888,”f”:null},{“v”:112,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.72″,”f”:null},{“v”:883,”f”:null},{“v”:117,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.73″,”f”:null},{“v”:878,”f”:null},{“v”:122,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.74″,”f”:null},{“v”:872,”f”:null},{“v”:128,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.75″,”f”:null},{“v”:866,”f”:null},{“v”:134,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.76″,”f”:null},{“v”:860,”f”:null},{“v”:140,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.77″,”f”:null},{“v”:853,”f”:null},{“v”:147,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.78″,”f”:null},{“v”:845,”f”:null},{“v”:155,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.79″,”f”:null},{“v”:838,”f”:null},{“v”:162,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.8″,”f”:null},{“v”:829,”f”:null},{“v”:171,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.81″,”f”:null},{“v”:820,”f”:null},{“v”:180,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.82″,”f”:null},{“v”:810,”f”:null},{“v”:190,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.83″,”f”:null},{“v”:799,”f”:null},{“v”:201,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.84″,”f”:null},{“v”:787,”f”:null},{“v”:213,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.85″,”f”:null},{“v”:774,”f”:null},{“v”:226,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.86″,”f”:null},{“v”:760,”f”:null},{“v”:240,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.87″,”f”:null},{“v”:744,”f”:null},{“v”:256,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.88″,”f”:null},{“v”:726,”f”:null},{“v”:274,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.89″,”f”:null},{“v”:706,”f”:null},{“v”:294,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.9″,”f”:null},{“v”:683,”f”:null},{“v”:317,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.91″,”f”:null},{“v”:657,”f”:null},{“v”:343,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.92″,”f”:null},{“v”:628,”f”:null},{“v”:372,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.93″,”f”:null},{“v”:594,”f”:null},{“v”:406,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.94″,”f”:null},{“v”:553,”f”:null},{“v”:447,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.95″,”f”:null},{“v”:505,”f”:null},{“v”:495,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.96″,”f”:null},{“v”:447,”f”:null},{“v”:553,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.97″,”f”:null},{“v”:375,”f”:null},{“v”:625,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.98″,”f”:null},{“v”:284,”f”:null},{“v”:716,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.99″,”f”:null},{“v”:164,”f”:null},{“v”:836,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”1″,”f”:null},{“v”:0,”f”:null},{“v”:1000,”f”:null}xxx01xxx}xxx01xxx,”p”:null},”options”:{“legend”:”top”,”title”:”Interpreting negative results”,”isStacked”:true,”vAxes”:xxx00xxx{“title”:”Number of people”,”minValue”:null,”maxValue”:null,”viewWindow”:{“max”:null,”min”:null},”logScale”:false,”useFormatFromData”:true},{“viewWindow”:{“max”:null,”min”:null},”minValue”:null,”maxValue”:null,”logScale”:false,”useFormatFromData”:true}xxx01xxx,”animation”:{“duration”:500},”booleanRole”:”certainty”,”hAxis”:{“minValue”:null,”maxValue”:null,”viewWindow”:null,”viewWindowMode”:null,”useFormatFromData”:true,”title”:”Baseline risk (prior – P(H))”},”series”:{“0”:{“color”:”#00b1b1″,”areaOpacity”:”0.3″},”1″:{“color”:”#cc0000″,”areaOpacity”:”0.3″}}},”state”:{},”view”:{},”isDefaultVisualization”:false,”chartType”:”AreaChart”}’ ]
That’s the value of testing from the perspective of someone who has, or hasn’t tested positive. The public health perspective is to ask how many people would be in each of the four quadrants of our table if we tested everyone. Again, this depends very heavily on ![]() :
:
Graph 3
[chartboot version= ‘3.0’ code= ‘E0AA’ border= ‘1’ width= ‘800’ height= ‘400’ attribution= ‘1’ jsondesc= ‘{“containerId”:”visualizationE0AA”,”dataTable”:{“cols”:xxx00xxx{“id”:””,”label”:””,”pattern”:””,”type”:”string”,”p”:{}},{“id”:””,”label”:”False negative”,”pattern”:””,”type”:”number”,”p”:{}},{“id”:””,”label”:”False positive”,”pattern”:””,”type”:”number”,”p”:{}},{“id”:””,”label”:”True negative”,”pattern”:””,”type”:”number”,”p”:{}},{“id”:””,”label”:”True positive”,”pattern”:””,”type”:”number”}xxx01xxx,”rows”:xxx00xxx{“c”:xxx00xxx{“v”:”0″,”f”:null},{“v”:0,”f”:null},{“v”:30,”f”:null},{“v”:970,”f”:null},{“v”:0,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.01″,”f”:null},{“v”:1,”f”:null},{“v”:30,”f”:null},{“v”:960,”f”:null},{“v”:10,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.02″,”f”:null},{“v”:1,”f”:null},{“v”:29,”f”:null},{“v”:951,”f”:null},{“v”:19,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.03″,”f”:null},{“v”:2,”f”:null},{“v”:29,”f”:null},{“v”:941,”f”:null},{“v”:29,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.04″,”f”:null},{“v”:2,”f”:null},{“v”:29,”f”:null},{“v”:931,”f”:null},{“v”:38,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.05″,”f”:null},{“v”:3,”f”:null},{“v”:29,”f”:null},{“v”:922,”f”:null},{“v”:48,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.06″,”f”:null},{“v”:3,”f”:null},{“v”:28,”f”:null},{“v”:912,”f”:null},{“v”:57,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.07″,”f”:null},{“v”:4,”f”:null},{“v”:28,”f”:null},{“v”:902,”f”:null},{“v”:67,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.08″,”f”:null},{“v”:4,”f”:null},{“v”:28,”f”:null},{“v”:892,”f”:null},{“v”:76,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.09″,”f”:null},{“v”:5,”f”:null},{“v”:27,”f”:null},{“v”:883,”f”:null},{“v”:86,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.1″,”f”:null},{“v”:5,”f”:null},{“v”:27,”f”:null},{“v”:873,”f”:null},{“v”:95,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.11″,”f”:null},{“v”:6,”f”:null},{“v”:27,”f”:null},{“v”:863,”f”:null},{“v”:105,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.12″,”f”:null},{“v”:6,”f”:null},{“v”:26,”f”:null},{“v”:854,”f”:null},{“v”:114,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.13″,”f”:null},{“v”:7,”f”:null},{“v”:26,”f”:null},{“v”:844,”f”:null},{“v”:124,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.14″,”f”:null},{“v”:7,”f”:null},{“v”:26,”f”:null},{“v”:834,”f”:null},{“v”:133,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.15″,”f”:null},{“v”:8,”f”:null},{“v”:26,”f”:null},{“v”:825,”f”:null},{“v”:143,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.16″,”f”:null},{“v”:8,”f”:null},{“v”:25,”f”:null},{“v”:815,”f”:null},{“v”:152,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.17″,”f”:null},{“v”:9,”f”:null},{“v”:25,”f”:null},{“v”:805,”f”:null},{“v”:162,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.18″,”f”:null},{“v”:9,”f”:null},{“v”:25,”f”:null},{“v”:795,”f”:null},{“v”:171,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.19″,”f”:null},{“v”:10,”f”:null},{“v”:24,”f”:null},{“v”:786,”f”:null},{“v”:181,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.2″,”f”:null},{“v”:10,”f”:null},{“v”:24,”f”:null},{“v”:776,”f”:null},{“v”:190,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.21″,”f”:null},{“v”:11,”f”:null},{“v”:24,”f”:null},{“v”:766,”f”:null},{“v”:200,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.22″,”f”:null},{“v”:11,”f”:null},{“v”:23,”f”:null},{“v”:757,”f”:null},{“v”:209,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.23″,”f”:null},{“v”:12,”f”:null},{“v”:23,”f”:null},{“v”:747,”f”:null},{“v”:219,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.24″,”f”:null},{“v”:12,”f”:null},{“v”:23,”f”:null},{“v”:737,”f”:null},{“v”:228,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.25″,”f”:null},{“v”:13,”f”:null},{“v”:23,”f”:null},{“v”:728,”f”:null},{“v”:238,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.26″,”f”:null},{“v”:13,”f”:null},{“v”:22,”f”:null},{“v”:718,”f”:null},{“v”:247,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.27″,”f”:null},{“v”:14,”f”:null},{“v”:22,”f”:null},{“v”:708,”f”:null},{“v”:257,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.28″,”f”:null},{“v”:14,”f”:null},{“v”:22,”f”:null},{“v”:698,”f”:null},{“v”:266,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.29″,”f”:null},{“v”:15,”f”:null},{“v”:21,”f”:null},{“v”:689,”f”:null},{“v”:276,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.3″,”f”:null},{“v”:15,”f”:null},{“v”:21,”f”:null},{“v”:679,”f”:null},{“v”:285,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.31″,”f”:null},{“v”:16,”f”:null},{“v”:21,”f”:null},{“v”:669,”f”:null},{“v”:295,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.32″,”f”:null},{“v”:16,”f”:null},{“v”:20,”f”:null},{“v”:660,”f”:null},{“v”:304,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.33″,”f”:null},{“v”:17,”f”:null},{“v”:20,”f”:null},{“v”:650,”f”:null},{“v”:314,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.34″,”f”:null},{“v”:17,”f”:null},{“v”:20,”f”:null},{“v”:640,”f”:null},{“v”:323,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.35″,”f”:null},{“v”:18,”f”:null},{“v”:20,”f”:null},{“v”:631,”f”:null},{“v”:333,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.36″,”f”:null},{“v”:18,”f”:null},{“v”:19,”f”:null},{“v”:621,”f”:null},{“v”:342,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.37″,”f”:null},{“v”:19,”f”:null},{“v”:19,”f”:null},{“v”:611,”f”:null},{“v”:352,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.38″,”f”:null},{“v”:19,”f”:null},{“v”:19,”f”:null},{“v”:601,”f”:null},{“v”:361,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.39″,”f”:null},{“v”:20,”f”:null},{“v”:18,”f”:null},{“v”:592,”f”:null},{“v”:371,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.4″,”f”:null},{“v”:20,”f”:null},{“v”:18,”f”:null},{“v”:582,”f”:null},{“v”:380,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.41″,”f”:null},{“v”:21,”f”:null},{“v”:18,”f”:null},{“v”:572,”f”:null},{“v”:390,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.42″,”f”:null},{“v”:21,”f”:null},{“v”:17,”f”:null},{“v”:563,”f”:null},{“v”:399,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.43″,”f”:null},{“v”:22,”f”:null},{“v”:17,”f”:null},{“v”:553,”f”:null},{“v”:409,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.44″,”f”:null},{“v”:22,”f”:null},{“v”:17,”f”:null},{“v”:543,”f”:null},{“v”:418,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.45″,”f”:null},{“v”:23,”f”:null},{“v”:17,”f”:null},{“v”:534,”f”:null},{“v”:428,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.46″,”f”:null},{“v”:23,”f”:null},{“v”:16,”f”:null},{“v”:524,”f”:null},{“v”:437,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.47″,”f”:null},{“v”:24,”f”:null},{“v”:16,”f”:null},{“v”:514,”f”:null},{“v”:447,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.48″,”f”:null},{“v”:24,”f”:null},{“v”:16,”f”:null},{“v”:504,”f”:null},{“v”:456,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.49″,”f”:null},{“v”:25,”f”:null},{“v”:15,”f”:null},{“v”:495,”f”:null},{“v”:466,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.5″,”f”:null},{“v”:25,”f”:null},{“v”:15,”f”:null},{“v”:485,”f”:null},{“v”:475,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.51″,”f”:null},{“v”:26,”f”:null},{“v”:15,”f”:null},{“v”:475,”f”:null},{“v”:485,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.52″,”f”:null},{“v”:26,”f”:null},{“v”:14,”f”:null},{“v”:466,”f”:null},{“v”:494,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.53″,”f”:null},{“v”:27,”f”:null},{“v”:14,”f”:null},{“v”:456,”f”:null},{“v”:504,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.54″,”f”:null},{“v”:27,”f”:null},{“v”:14,”f”:null},{“v”:446,”f”:null},{“v”:513,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.55″,”f”:null},{“v”:28,”f”:null},{“v”:14,”f”:null},{“v”:437,”f”:null},{“v”:523,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.56″,”f”:null},{“v”:28,”f”:null},{“v”:13,”f”:null},{“v”:427,”f”:null},{“v”:532,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.57″,”f”:null},{“v”:29,”f”:null},{“v”:13,”f”:null},{“v”:417,”f”:null},{“v”:542,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.58″,”f”:null},{“v”:29,”f”:null},{“v”:13,”f”:null},{“v”:407,”f”:null},{“v”:551,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.59″,”f”:null},{“v”:30,”f”:null},{“v”:12,”f”:null},{“v”:398,”f”:null},{“v”:561,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.6″,”f”:null},{“v”:30,”f”:null},{“v”:12,”f”:null},{“v”:388,”f”:null},{“v”:570,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.61″,”f”:null},{“v”:31,”f”:null},{“v”:12,”f”:null},{“v”:378,”f”:null},{“v”:580,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.62″,”f”:null},{“v”:31,”f”:null},{“v”:11,”f”:null},{“v”:369,”f”:null},{“v”:589,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.63″,”f”:null},{“v”:32,”f”:null},{“v”:11,”f”:null},{“v”:359,”f”:null},{“v”:599,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.64″,”f”:null},{“v”:32,”f”:null},{“v”:11,”f”:null},{“v”:349,”f”:null},{“v”:608,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.65″,”f”:null},{“v”:33,”f”:null},{“v”:11,”f”:null},{“v”:340,”f”:null},{“v”:618,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.66″,”f”:null},{“v”:33,”f”:null},{“v”:10,”f”:null},{“v”:330,”f”:null},{“v”:627,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.67″,”f”:null},{“v”:34,”f”:null},{“v”:10,”f”:null},{“v”:320,”f”:null},{“v”:637,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.68″,”f”:null},{“v”:34,”f”:null},{“v”:10,”f”:null},{“v”:310,”f”:null},{“v”:646,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.69″,”f”:null},{“v”:35,”f”:null},{“v”:9,”f”:null},{“v”:301,”f”:null},{“v”:656,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.7″,”f”:null},{“v”:35,”f”:null},{“v”:9,”f”:null},{“v”:291,”f”:null},{“v”:665,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.71″,”f”:null},{“v”:36,”f”:null},{“v”:9,”f”:null},{“v”:281,”f”:null},{“v”:675,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.72″,”f”:null},{“v”:36,”f”:null},{“v”:8,”f”:null},{“v”:272,”f”:null},{“v”:684,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.73″,”f”:null},{“v”:37,”f”:null},{“v”:8,”f”:null},{“v”:262,”f”:null},{“v”:694,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.74″,”f”:null},{“v”:37,”f”:null},{“v”:8,”f”:null},{“v”:252,”f”:null},{“v”:703,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.75″,”f”:null},{“v”:38,”f”:null},{“v”:8,”f”:null},{“v”:243,”f”:null},{“v”:713,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.76″,”f”:null},{“v”:38,”f”:null},{“v”:7,”f”:null},{“v”:233,”f”:null},{“v”:722,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.77″,”f”:null},{“v”:39,”f”:null},{“v”:7,”f”:null},{“v”:223,”f”:null},{“v”:732,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.78″,”f”:null},{“v”:39,”f”:null},{“v”:7,”f”:null},{“v”:213,”f”:null},{“v”:741,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.79″,”f”:null},{“v”:40,”f”:null},{“v”:6,”f”:null},{“v”:204,”f”:null},{“v”:751,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.8″,”f”:null},{“v”:40,”f”:null},{“v”:6,”f”:null},{“v”:194,”f”:null},{“v”:760,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.81″,”f”:null},{“v”:41,”f”:null},{“v”:6,”f”:null},{“v”:184,”f”:null},{“v”:770,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.82″,”f”:null},{“v”:41,”f”:null},{“v”:5,”f”:null},{“v”:175,”f”:null},{“v”:779,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.83″,”f”:null},{“v”:42,”f”:null},{“v”:5,”f”:null},{“v”:165,”f”:null},{“v”:789,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.84″,”f”:null},{“v”:42,”f”:null},{“v”:5,”f”:null},{“v”:155,”f”:null},{“v”:798,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.85″,”f”:null},{“v”:43,”f”:null},{“v”:5,”f”:null},{“v”:146,”f”:null},{“v”:808,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.86″,”f”:null},{“v”:43,”f”:null},{“v”:4,”f”:null},{“v”:136,”f”:null},{“v”:817,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.87″,”f”:null},{“v”:44,”f”:null},{“v”:4,”f”:null},{“v”:126,”f”:null},{“v”:827,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.88″,”f”:null},{“v”:44,”f”:null},{“v”:4,”f”:null},{“v”:116,”f”:null},{“v”:836,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.89″,”f”:null},{“v”:45,”f”:null},{“v”:3,”f”:null},{“v”:107,”f”:null},{“v”:846,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.9″,”f”:null},{“v”:45,”f”:null},{“v”:3,”f”:null},{“v”:97,”f”:null},{“v”:855,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.91″,”f”:null},{“v”:46,”f”:null},{“v”:3,”f”:null},{“v”:87,”f”:null},{“v”:865,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.92″,”f”:null},{“v”:46,”f”:null},{“v”:2,”f”:null},{“v”:78,”f”:null},{“v”:874,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.93″,”f”:null},{“v”:47,”f”:null},{“v”:2,”f”:null},{“v”:68,”f”:null},{“v”:884,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.94″,”f”:null},{“v”:47,”f”:null},{“v”:2,”f”:null},{“v”:58,”f”:null},{“v”:893,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.95″,”f”:null},{“v”:48,”f”:null},{“v”:2,”f”:null},{“v”:49,”f”:null},{“v”:903,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.96″,”f”:null},{“v”:48,”f”:null},{“v”:1,”f”:null},{“v”:39,”f”:null},{“v”:912,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.97″,”f”:null},{“v”:49,”f”:null},{“v”:1,”f”:null},{“v”:29,”f”:null},{“v”:922,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.98″,”f”:null},{“v”:49,”f”:null},{“v”:1,”f”:null},{“v”:19,”f”:null},{“v”:931,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.99″,”f”:null},{“v”:50,”f”:null},{“v”:0,”f”:null},{“v”:10,”f”:null},{“v”:941,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”1″,”f”:null},{“v”:50,”f”:null},{“v”:0,”f”:null},{“v”:0,”f”:null},{“v”:950,”f”:null}xxx01xxx}xxx01xxx,”p”:null},”options”:{“legend”:”right”,”title”:”The public health perspective”,”isStacked”:true,”vAxes”:xxx00xxx{“title”:”Number of people”,”minValue”:null,”maxValue”:1000,”viewWindow”:{“max”:1000,”min”:null},”logScale”:false,”useFormatFromData”:true,”viewWindowMode”:”explicit”},{“viewWindow”:{“max”:null,”min”:null},”minValue”:null,”maxValue”:null,”logScale”:false,”useFormatFromData”:true}xxx01xxx,”animation”:{“duration”:500},”booleanRole”:”certainty”,”hAxis”:{“minValue”:null,”maxValue”:null,”viewWindow”:null,”viewWindowMode”:null,”useFormatFromData”:true,”title”:”Baseline risk (prior – P(H))”},”series”:{“0”:{“color”:”#cc0000″,”areaOpacity”:”0.5″},”1″:{“color”:”#ff9900″,”areaOpacity”:”0.5″},”2″:{“color”:”#00b1b1″,”areaOpacity”:”0.5″},”3″:{“color”:”#00cc7a”,”areaOpacity”:”0.5″}}},”state”:{},”view”:{},”isDefaultVisualization”:false,”chartType”:”AreaChart”}’ ]
If you look at these graphs, you will see that the value of testing is highly dependent on ![]() . The tests themselves are actually pretty good but, if you start using them on everyone, you will get a lot of false positives. In addition, when the risk of disease is very high, even low error rates result in cases being missed, with potentially serious consequences.
. The tests themselves are actually pretty good but, if you start using them on everyone, you will get a lot of false positives. In addition, when the risk of disease is very high, even low error rates result in cases being missed, with potentially serious consequences.
The arguments
The graphs above immediately tell us two things:
- Do not rely on testing alone – In high-risk environments, quarantine is necessary to prevent disease spread. However, most environments are not high-risk.
- Testing should not be used in very low-risk groups – The use of resource in testing will be huge for a very small benefit, and it may provide an illusion of protection.
Number 1. causes issues with healthcare staff. Essentially, maintaining frontline staffing is a huge challenge because it is difficult to be sure that someone in a high-risk environment doesn’t have disease. This means providing external frontline staff creates a risk of disease spread. For this reason (and others), a lot of international support is based around protecting and supporting healthcare professionals rather than providing frontline care.
Number 2. means that pre-screening is necessary. This is the reason that all screening programmes include more than just testing. They include questionnaires about exposure (e.g. ‘have you been in contact with anyone with ebola?’) and, sometimes, external signs of illness (e.g. raised body temperature). What pre-screening does is to identify people at increased baseline risk prior to more formal testing.
The main arguments about screening arise because of the sensitivity of testing to baseline risk. The argument is essentially whether the pre-screens used can identify people with a high baseline risk. There are several drivers of this.
One of the most important, and one that varies between different disease outbreaks, is the real risk of people flying into a country. When there is an outbreak of a disease like ebola, affected countries (or, at least, airlines using them) will check people boarding flights for signs of illness. The question is, what is the real risk of someone who isn’t showing signs on boarding developing sufficient signs for them to be picked up during the pre-screen once they land. This argument is complicated by things like whether people will try and hide illness to escape a high-risk area, any corruption amongst the people doing screening at boarding etc.
The issue of pre-screening is hugely important, because we have already seen that false positives and false negatives exist. False negatives during pre-screening mean a person never gets a proper test. Now, asking people a few questions and/or taking their temperature is probably not very sensitive (ebola has an incubation period with no raised temperature) or specific (all sorts of people get sick for all sorts of reasons. Let’s say the sensitivity and specificity of this pre-screen are both 50%. What does this do to our chart? This is what it does:
[chartboot version= ‘3.0’ code= ‘E884’ border= ‘1’ width= ‘800’ height= ‘400’ attribution= ‘1’ jsondesc= ‘{“containerId”:”visualizationE884″,”dataTable”:{“cols”:xxx00xxx{“id”:””,”label”:””,”pattern”:””,”type”:”string”,”p”:{}},{“id”:””,”label”:”False negative”,”pattern”:””,”type”:”number”,”p”:{}},{“id”:””,”label”:”False positive”,”pattern”:””,”type”:”number”,”p”:{}},{“id”:””,”label”:”True negative”,”pattern”:””,”type”:”number”,”p”:{}},{“id”:””,”label”:”True positive”,”pattern”:””,”type”:”number”}xxx01xxx,”rows”:xxx00xxx{“c”:xxx00xxx{“v”:”0″,”f”:null},{“v”:0,”f”:null},{“v”:500,”f”:null},{“v”:500,”f”:null},{“v”:0,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.01″,”f”:null},{“v”:5,”f”:null},{“v”:495,”f”:null},{“v”:495,”f”:null},{“v”:5,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.02″,”f”:null},{“v”:10,”f”:null},{“v”:490,”f”:null},{“v”:490,”f”:null},{“v”:10,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.03″,”f”:null},{“v”:15,”f”:null},{“v”:485,”f”:null},{“v”:485,”f”:null},{“v”:15,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.04″,”f”:null},{“v”:20,”f”:null},{“v”:480,”f”:null},{“v”:480,”f”:null},{“v”:20,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.05″,”f”:null},{“v”:25,”f”:null},{“v”:475,”f”:null},{“v”:475,”f”:null},{“v”:25,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.06″,”f”:null},{“v”:30,”f”:null},{“v”:470,”f”:null},{“v”:470,”f”:null},{“v”:30,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.07″,”f”:null},{“v”:35,”f”:null},{“v”:465,”f”:null},{“v”:465,”f”:null},{“v”:35,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.08″,”f”:null},{“v”:40,”f”:null},{“v”:460,”f”:null},{“v”:460,”f”:null},{“v”:40,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.09″,”f”:null},{“v”:45,”f”:null},{“v”:455,”f”:null},{“v”:455,”f”:null},{“v”:45,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.1″,”f”:null},{“v”:50,”f”:null},{“v”:450,”f”:null},{“v”:450,”f”:null},{“v”:50,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.11″,”f”:null},{“v”:55,”f”:null},{“v”:445,”f”:null},{“v”:445,”f”:null},{“v”:55,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.12″,”f”:null},{“v”:60,”f”:null},{“v”:440,”f”:null},{“v”:440,”f”:null},{“v”:60,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.13″,”f”:null},{“v”:65,”f”:null},{“v”:435,”f”:null},{“v”:435,”f”:null},{“v”:65,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.14″,”f”:null},{“v”:70,”f”:null},{“v”:430,”f”:null},{“v”:430,”f”:null},{“v”:70,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.15″,”f”:null},{“v”:75,”f”:null},{“v”:425,”f”:null},{“v”:425,”f”:null},{“v”:75,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.16″,”f”:null},{“v”:80,”f”:null},{“v”:420,”f”:null},{“v”:420,”f”:null},{“v”:80,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.17″,”f”:null},{“v”:85,”f”:null},{“v”:415,”f”:null},{“v”:415,”f”:null},{“v”:85,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.18″,”f”:null},{“v”:90,”f”:null},{“v”:410,”f”:null},{“v”:410,”f”:null},{“v”:90,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.19″,”f”:null},{“v”:95,”f”:null},{“v”:405,”f”:null},{“v”:405,”f”:null},{“v”:95,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.2″,”f”:null},{“v”:100,”f”:null},{“v”:400,”f”:null},{“v”:400,”f”:null},{“v”:100,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.21″,”f”:null},{“v”:105,”f”:null},{“v”:395,”f”:null},{“v”:395,”f”:null},{“v”:105,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.22″,”f”:null},{“v”:110,”f”:null},{“v”:390,”f”:null},{“v”:390,”f”:null},{“v”:110,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.23″,”f”:null},{“v”:115,”f”:null},{“v”:385,”f”:null},{“v”:385,”f”:null},{“v”:115,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.24″,”f”:null},{“v”:120,”f”:null},{“v”:380,”f”:null},{“v”:380,”f”:null},{“v”:120,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.25″,”f”:null},{“v”:125,”f”:null},{“v”:375,”f”:null},{“v”:375,”f”:null},{“v”:125,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.26″,”f”:null},{“v”:130,”f”:null},{“v”:370,”f”:null},{“v”:370,”f”:null},{“v”:130,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.27″,”f”:null},{“v”:135,”f”:null},{“v”:365,”f”:null},{“v”:365,”f”:null},{“v”:135,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.28″,”f”:null},{“v”:140,”f”:null},{“v”:360,”f”:null},{“v”:360,”f”:null},{“v”:140,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.29″,”f”:null},{“v”:145,”f”:null},{“v”:355,”f”:null},{“v”:355,”f”:null},{“v”:145,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.3″,”f”:null},{“v”:150,”f”:null},{“v”:350,”f”:null},{“v”:350,”f”:null},{“v”:150,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.31″,”f”:null},{“v”:155,”f”:null},{“v”:345,”f”:null},{“v”:345,”f”:null},{“v”:155,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.32″,”f”:null},{“v”:160,”f”:null},{“v”:340,”f”:null},{“v”:340,”f”:null},{“v”:160,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.33″,”f”:null},{“v”:165,”f”:null},{“v”:335,”f”:null},{“v”:335,”f”:null},{“v”:165,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.34″,”f”:null},{“v”:170,”f”:null},{“v”:330,”f”:null},{“v”:330,”f”:null},{“v”:170,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.35″,”f”:null},{“v”:175,”f”:null},{“v”:325,”f”:null},{“v”:325,”f”:null},{“v”:175,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.36″,”f”:null},{“v”:180,”f”:null},{“v”:320,”f”:null},{“v”:320,”f”:null},{“v”:180,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.37″,”f”:null},{“v”:185,”f”:null},{“v”:315,”f”:null},{“v”:315,”f”:null},{“v”:185,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.38″,”f”:null},{“v”:190,”f”:null},{“v”:310,”f”:null},{“v”:310,”f”:null},{“v”:190,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.39″,”f”:null},{“v”:195,”f”:null},{“v”:305,”f”:null},{“v”:305,”f”:null},{“v”:195,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.4″,”f”:null},{“v”:200,”f”:null},{“v”:300,”f”:null},{“v”:300,”f”:null},{“v”:200,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.41″,”f”:null},{“v”:205,”f”:null},{“v”:295,”f”:null},{“v”:295,”f”:null},{“v”:205,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.42″,”f”:null},{“v”:210,”f”:null},{“v”:290,”f”:null},{“v”:290,”f”:null},{“v”:210,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.43″,”f”:null},{“v”:215,”f”:null},{“v”:285,”f”:null},{“v”:285,”f”:null},{“v”:215,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.44″,”f”:null},{“v”:220,”f”:null},{“v”:280,”f”:null},{“v”:280,”f”:null},{“v”:220,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.45″,”f”:null},{“v”:225,”f”:null},{“v”:275,”f”:null},{“v”:275,”f”:null},{“v”:225,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.46″,”f”:null},{“v”:230,”f”:null},{“v”:270,”f”:null},{“v”:270,”f”:null},{“v”:230,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.47″,”f”:null},{“v”:235,”f”:null},{“v”:265,”f”:null},{“v”:265,”f”:null},{“v”:235,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.48″,”f”:null},{“v”:240,”f”:null},{“v”:260,”f”:null},{“v”:260,”f”:null},{“v”:240,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.49″,”f”:null},{“v”:245,”f”:null},{“v”:255,”f”:null},{“v”:255,”f”:null},{“v”:245,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.5″,”f”:null},{“v”:250,”f”:null},{“v”:250,”f”:null},{“v”:250,”f”:null},{“v”:250,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.51″,”f”:null},{“v”:255,”f”:null},{“v”:245,”f”:null},{“v”:245,”f”:null},{“v”:255,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.52″,”f”:null},{“v”:260,”f”:null},{“v”:240,”f”:null},{“v”:240,”f”:null},{“v”:260,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.53″,”f”:null},{“v”:265,”f”:null},{“v”:235,”f”:null},{“v”:235,”f”:null},{“v”:265,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.54″,”f”:null},{“v”:270,”f”:null},{“v”:230,”f”:null},{“v”:230,”f”:null},{“v”:270,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.55″,”f”:null},{“v”:275,”f”:null},{“v”:225,”f”:null},{“v”:225,”f”:null},{“v”:275,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.56″,”f”:null},{“v”:280,”f”:null},{“v”:220,”f”:null},{“v”:220,”f”:null},{“v”:280,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.57″,”f”:null},{“v”:285,”f”:null},{“v”:215,”f”:null},{“v”:215,”f”:null},{“v”:285,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.58″,”f”:null},{“v”:290,”f”:null},{“v”:210,”f”:null},{“v”:210,”f”:null},{“v”:290,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.59″,”f”:null},{“v”:295,”f”:null},{“v”:205,”f”:null},{“v”:205,”f”:null},{“v”:295,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.6″,”f”:null},{“v”:300,”f”:null},{“v”:200,”f”:null},{“v”:200,”f”:null},{“v”:300,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.61″,”f”:null},{“v”:305,”f”:null},{“v”:195,”f”:null},{“v”:195,”f”:null},{“v”:305,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.62″,”f”:null},{“v”:310,”f”:null},{“v”:190,”f”:null},{“v”:190,”f”:null},{“v”:310,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.63″,”f”:null},{“v”:315,”f”:null},{“v”:185,”f”:null},{“v”:185,”f”:null},{“v”:315,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.64″,”f”:null},{“v”:320,”f”:null},{“v”:180,”f”:null},{“v”:180,”f”:null},{“v”:320,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.65″,”f”:null},{“v”:325,”f”:null},{“v”:175,”f”:null},{“v”:175,”f”:null},{“v”:325,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.66″,”f”:null},{“v”:330,”f”:null},{“v”:170,”f”:null},{“v”:170,”f”:null},{“v”:330,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.67″,”f”:null},{“v”:335,”f”:null},{“v”:165,”f”:null},{“v”:165,”f”:null},{“v”:335,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.68″,”f”:null},{“v”:340,”f”:null},{“v”:160,”f”:null},{“v”:160,”f”:null},{“v”:340,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.69″,”f”:null},{“v”:345,”f”:null},{“v”:155,”f”:null},{“v”:155,”f”:null},{“v”:345,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.7″,”f”:null},{“v”:350,”f”:null},{“v”:150,”f”:null},{“v”:150,”f”:null},{“v”:350,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.71″,”f”:null},{“v”:355,”f”:null},{“v”:145,”f”:null},{“v”:145,”f”:null},{“v”:355,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.72″,”f”:null},{“v”:360,”f”:null},{“v”:140,”f”:null},{“v”:140,”f”:null},{“v”:360,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.73″,”f”:null},{“v”:365,”f”:null},{“v”:135,”f”:null},{“v”:135,”f”:null},{“v”:365,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.74″,”f”:null},{“v”:370,”f”:null},{“v”:130,”f”:null},{“v”:130,”f”:null},{“v”:370,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.75″,”f”:null},{“v”:375,”f”:null},{“v”:125,”f”:null},{“v”:125,”f”:null},{“v”:375,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.76″,”f”:null},{“v”:380,”f”:null},{“v”:120,”f”:null},{“v”:120,”f”:null},{“v”:380,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.77″,”f”:null},{“v”:385,”f”:null},{“v”:115,”f”:null},{“v”:115,”f”:null},{“v”:385,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.78″,”f”:null},{“v”:390,”f”:null},{“v”:110,”f”:null},{“v”:110,”f”:null},{“v”:390,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.79″,”f”:null},{“v”:395,”f”:null},{“v”:105,”f”:null},{“v”:105,”f”:null},{“v”:395,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.8″,”f”:null},{“v”:400,”f”:null},{“v”:100,”f”:null},{“v”:100,”f”:null},{“v”:400,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.81″,”f”:null},{“v”:405,”f”:null},{“v”:95,”f”:null},{“v”:95,”f”:null},{“v”:405,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.82″,”f”:null},{“v”:410,”f”:null},{“v”:90,”f”:null},{“v”:90,”f”:null},{“v”:410,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.83″,”f”:null},{“v”:415,”f”:null},{“v”:85,”f”:null},{“v”:85,”f”:null},{“v”:415,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.84″,”f”:null},{“v”:420,”f”:null},{“v”:80,”f”:null},{“v”:80,”f”:null},{“v”:420,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.85″,”f”:null},{“v”:425,”f”:null},{“v”:75,”f”:null},{“v”:75,”f”:null},{“v”:425,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.86″,”f”:null},{“v”:430,”f”:null},{“v”:70,”f”:null},{“v”:70,”f”:null},{“v”:430,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.87″,”f”:null},{“v”:435,”f”:null},{“v”:65,”f”:null},{“v”:65,”f”:null},{“v”:435,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.88″,”f”:null},{“v”:440,”f”:null},{“v”:60,”f”:null},{“v”:60,”f”:null},{“v”:440,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.89″,”f”:null},{“v”:445,”f”:null},{“v”:55,”f”:null},{“v”:55,”f”:null},{“v”:445,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.9″,”f”:null},{“v”:450,”f”:null},{“v”:50,”f”:null},{“v”:50,”f”:null},{“v”:450,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.91″,”f”:null},{“v”:455,”f”:null},{“v”:45,”f”:null},{“v”:45,”f”:null},{“v”:455,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.92″,”f”:null},{“v”:460,”f”:null},{“v”:40,”f”:null},{“v”:40,”f”:null},{“v”:460,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.93″,”f”:null},{“v”:465,”f”:null},{“v”:35,”f”:null},{“v”:35,”f”:null},{“v”:465,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.94″,”f”:null},{“v”:470,”f”:null},{“v”:30,”f”:null},{“v”:30,”f”:null},{“v”:470,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.95″,”f”:null},{“v”:475,”f”:null},{“v”:25,”f”:null},{“v”:25,”f”:null},{“v”:475,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.96″,”f”:null},{“v”:480,”f”:null},{“v”:20,”f”:null},{“v”:20,”f”:null},{“v”:480,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.97″,”f”:null},{“v”:485,”f”:null},{“v”:15,”f”:null},{“v”:15,”f”:null},{“v”:485,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.98″,”f”:null},{“v”:490,”f”:null},{“v”:10,”f”:null},{“v”:10,”f”:null},{“v”:490,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”0.99″,”f”:null},{“v”:495,”f”:null},{“v”:5,”f”:null},{“v”:5,”f”:null},{“v”:495,”f”:null}xxx01xxx},{“c”:xxx00xxx{“v”:”1″,”f”:null},{“v”:500,”f”:null},{“v”:0,”f”:null},{“v”:0,”f”:null},{“v”:500,”f”:null}xxx01xxx}xxx01xxx,”p”:null},”options”:{“legend”:”right”,”title”:”The problems of pre-screening”,”isStacked”:true,”vAxes”:xxx00xxx{“title”:”Number of people”,”minValue”:null,”maxValue”:null,”viewWindow”:{“max”:null,”min”:null},”logScale”:false,”useFormatFromData”:true},{“viewWindow”:{“max”:null,”min”:null},”minValue”:null,”maxValue”:null,”logScale”:false,”useFormatFromData”:true}xxx01xxx,”animation”:{“duration”:500},”booleanRole”:”certainty”,”hAxis”:{“minValue”:null,”maxValue”:null,”viewWindow”:null,”viewWindowMode”:null,”useFormatFromData”:true,”title”:”Baseline risk (prior – P(H))”},”series”:{“0”:{“color”:”#cc0000″,”areaOpacity”:”0.5″},”1″:{“color”:”#ff9900″,”areaOpacity”:”0.5″},”2″:{“color”:”#00b1b1″,”areaOpacity”:”0.5″},”3″:{“color”:”#00cc7a”,”areaOpacity”:”0.5″}}},”state”:{},”view”:{},”isDefaultVisualization”:false,”chartType”:”AreaChart”}’ ]
This could be quite alarming. After all, it suggests that quite a few people could be missed. The point is that this stage is really sensitive to how the pre-screen is done. Do we accept a lot of people being inconvenienced (i.e. getting a false positive), and a consequent slow-down in international movement and huge cost to catch as many cases as possible (while still missing some)? Or do we use the pre-screen as an opportunity to inform higher-risk people of the signs of illness? Actually, this second approach can be important, if it means telling people leaving a high-risk area that reporting sickness is okay and will result in them getting good medical care.
The point is that the decisions involved in screening are complex. There is, undoubtedly, political pressure to do something, but there is logic behind some of the ineffective-sounding screening activities (questionnaires, temperature-testing etc.).
It’s all about the baseline risk, and that is very difficult to estimate. If you look at the shape of the graphs above, you will see that slight differences in that estimate may produce very different decisions about the value of screening.
That is why there are arguments and it is why those arguments are legitimate. Unfortunately, there is no simple answer. What Bayesian approaches can help us do is to agree a structure for those arguments so that, in difficult situations, we focus on the factors that should drive our decisions. While screening is a specialist area, by breaking the problem down into its component parts, it is possible for a non-specialist to engage in the discussion. That is surely better than relying on our natural trust (!) in official statements.
These things can get pretty complex quickly. That means I’ve probably got something wrong – what is it? Let me know below.

Leave a Reply
You must be logged in to post a comment.